
リピート率をあげたい!とECサイトの運営者では思うのではないでしょうか。このリピート率という数字を改善するにあたって色々な角度で見ることも必要です。
ベイズの定理は起きた結果から原因を推察し、その確率を算出するのに最適です。今回は基本的なベイズの定理について例をあげます。
ベイズの定理とは
まずベイズの定理とは何か。これは確率計算式のことで古くはナチスのエニグマの解読、米軍の核兵器開発で事故が起こる確率や行方不明の原子力潜水艦の捜索などに使われたそうです。この定理を元に「ある証拠からその原因となることを推察する」というベイズ推定やベイズ統計学というものがあります。
今回はそのベイズの定理を元にキャンペーン商品の購入でリピートにつながる確率を計算します。
計測される値を用意する
計算をする前に問題としてある「キャンペーン商品の購入でリピートにつながる確率を計算する」ための情報が必要です。
ECなどで管理しているデータを元に考えることができます。
・リピート率
・キャンペーン商品を購入した人がその後リピートした割合
・キャンペーン商品を購入していない人がその後リピートした割合
・キャンペーン商品を購入したが人がリピートしなかった割合
・キャンペーン商品を購入していない人がその後リピートしなかった割合
こういったところでしょうか。そしてその数字は以下のものだったとします。
リピート率は12%
| キャンペーン商品購入 | キャンペーン商品未購入 | |
| リピートした | 0.6 | 0.4 |
| リピートしてない | 0.2 | 0.8 |
この表はリピートの有無に対しての購入非購入の割合です。行の合計が1になりますが、列の合計は1にはなっていません。これはリピートした人での割合、リピートしていない人での割合ということであるため縦に一括りにできないのです。
ベイズの定理の公式に当てはめる
ベイスの定理には公式があります。
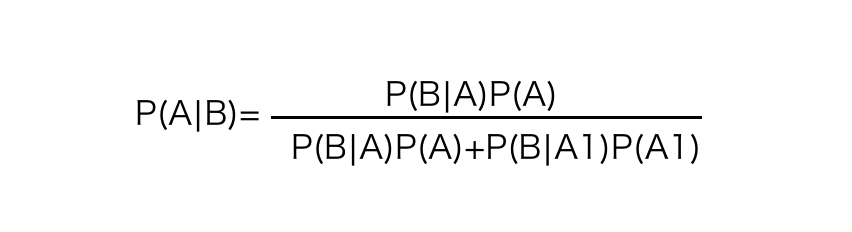
・左辺のP(A|B)とは「BであることでAである確率」になります。
・右辺の上段はP(A)は「Aである確率」、P(B|A)は「Aが起きることでBが起きる確率」を表します。つまりこれは「AかつBが起きる確率」を表します。
・右辺の下段はBが起きうる全ての確率の合計を表します。その中でP(B|A)P(A)は「AかつBが起きる確率」、そしてP(B|A1)P(A1)は「A1かつBが起きる確率」です。ここでAとA1は同時に起きることがない必要があります。
この式をこの問題に当てはまると以下のようになります。

・左辺は「キャンペーン商品を購入したことでリピートが発生する確率」を表します。
・右辺上段は「キャンペーン商品を購入し、かつリピートをする確率」を表します。
・右辺下段は「キャンペーン商品を購入する全確率」を表します。これは「キャンペーン商品を購入し、かつリピートをする確率」と「キャンペーン商品を購入し、かつリピートをしない確率」を合計したものです。
この式に準備をした値を当てはめて計算します。

・右辺上段P(A)の部分にはリピート率である0.12が入ります。この価は事前確率と呼ばれるものです。
・右辺上段P(B|A)部分はAかつBの確率、つまりここでは0.6が入ります。
・右辺下段には全てのP(B)が発生する確率、つまりAかつBの確率とA1かつBの確率が入ります。A1かつBとは「リピートしないかつキャンペーン商品を購入」の確率が入ります。ここでは0.6×0.12+0.2×0.88です。
よってこの式を計算すると約0.29となります。計算式の右辺は「リピートかつ商品購入した確率」を「商品購入した全ての確率」で割ったものであり、この場合の式では「キャンペーン商品を購入していない情報」は一切使いません。
このことから、何もしない場合のリピート率が12%だったものが、キャンペン商品の販売をすることで29%まで引き上がるということになります。
ベイスの定理を使うことでこれまでに「リピートが発生した結果」から「特定商品の購入」が原因となることを見ることができます。今回はあくまでもざっくりとした形での説明になりましたが、専門的にベイズ理論やベイズ統計を理解することができれば様々な形での確率を検証することができるのではないでしょうか。






Leave a Reply