
世の中には色々な出来事(事象)が起きます。それは自分でコントロールできることであれば問題ないのだけど、そうでない場合はその事象が自分にとってメリットがある場合、また逆にデメリットがある場合はどう判断すれば良いでしょうか。もし、それが確率で考えることができれば比較的容易に判断することができます。今回は事象の発生を判断するために理解しておくべき「確率変数」と「確率分布」について説明します。
確率変数とは
中学になり数学を勉強する上で、XやY、Zまたa,b,cといった記号を使った数式をいくつも解いてきたと思います。例えば
Y = 5 * X + 13 といった式の場合、Xが1の時Yは18、Xが2の時Yは23というように、Xに入る値でYの値も変わります。この決まった値ではないXやYなどを「変数」と呼びます。そしてこの変数が確率にしたがって決定するものを「確率変数」と呼びます。
例えば、6面体のサイコロですが降った時にでる目の値は1、2、3、4、5、6が出ます。サイコロの目が出る確率はそれぞれ1/6なので、同じ確率で全ての値が出ます。このことから出る目である1、2、3、4、5、6は確率変数です。これはいびつな形をして出る目に偏りがあるようなサイコロ(極端な例で言えば1が異常に出やすいイカサマ用サイコロ)であっても出る目の値は確率に従っているためXは確率変数となります。
| 普通のサイコロの場合 | ||||||
| 目の値(X) | 1 | 2 | 3 | 4 | 5 | 6 |
| 目の出る確率 | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 |
| 出る目の確率が極端なサイコロの場合 | ||||||
| 目の値(X) | 1 | 2 | 3 | 4 | 5 | 6 |
| 目の出る確率 | 1/2 | 1/10 | 1/10 | 1/10 | 1/10 | 1/10 |
上記の例はサイコロの出る目(確率変数Xに格納される実際の値)はどちらも同じですが、どちらのどの値も確率によって決定されることがわかります。
確率分布とは
上記の表で確率変数がどのくらいで発生するかの確率がわかっていると思います。その確率を見やすくまとめたものを確率分布と呼びます。
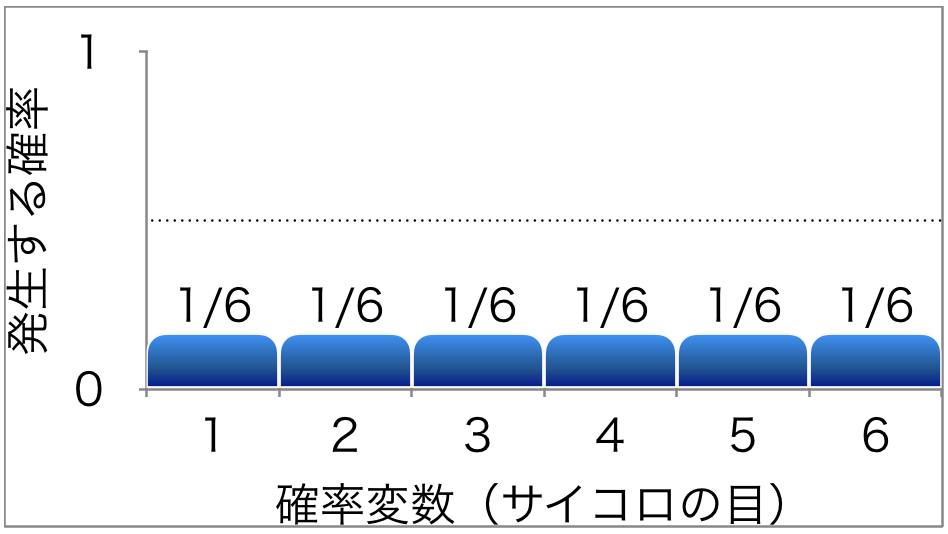
この図では普通のサイコロの確率をグラフで表しましたが、どの目も同じように1/6です。全ての合計が1つまり確率でいえば100%で、サイコロを振って出る目は全てこのグラフの中に収まります。
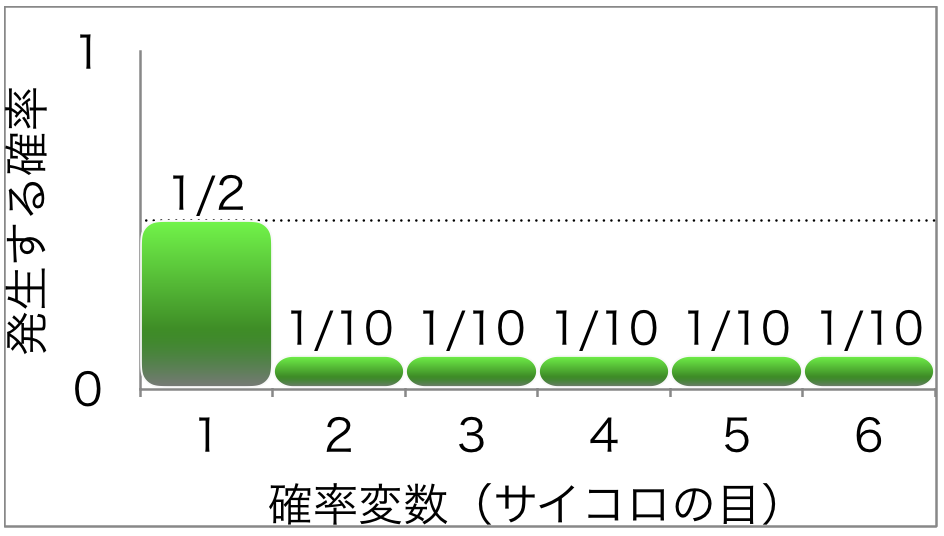
この図では出る目が極端なサイコロの確率をグラフにしたものです。グラフで見ると1の目が1/2の確率で、それ以外の目が1/10であることがわかります。これも全ての合計が1になり、サイコロを振って出る目はずべてこのグラフの中に収まります。
このことから確率分布とは確率変数のとる値と、その値をとる確率の全ての広がりであることがわかります。
確率分布でするベストな選択
では確率分布を知ることで、できることは何でしょうか。その一つに「検定」があります。ウェブサイトを効率的に改善する場合、ABテストを行うことがあります。このテストではいくつかのパターンを作り、クリック率やコンバージョン率のテストを行うのですが、そのテスト結果の検証に「検定」を行います。ルールに則った「検定」を行うことで主観で判断しがちなものを客観視することができるようになります。
このほか、確率分布を比較することで自分の求める結果が出やすい方を選ぶということもできます。例えば普通の立方体のサイコロと長方体のサイコロがあるとします。立方体のサイコロは全ての面が等しい確率で出ます。長方体のサイコロは3・4がよく出て、その次に2・5、1・6はあまり出ません。
| 普通のサイコロの場合 | ||||||
| 目の値(X) | 1 | 2 | 3 | 4 | 5 | 6 |
| 目の出る確率 | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 |
| 長方体のサイコロの場合 | ||||||
| 目の値(X) | 1 | 2 | 3 | 4 | 5 | 6 |
| 目の出る確率 | 1/12 | 1/6 | 1/4 | 1/4 | 1/6 | 1/12 |
もし出た目×10,000円もらえる場合、どちらのサイコロを選びますか?また、サイコロを1回振るのに参加費が20,000円かかる場合どちらのサイコロを選びますか?参加費を払う必要がある場合、普通のサイコロで損をする1がでる確率は1/6、長方体のサイコロでは1/12です。損も得もしない2が出る確率は普通のサイコロで1/6、長方体は1/6です。このことから普通のサイコロでお金がもらえる確率は4/6で、長方体のサイコロでは9/12です。
逆に考えて高額となる5・6が出る確率は普通のサイコロで2/6、長方体のサイコロで3/12です。このことから高額を狙う場合は普通のサイコロで、安定してお金が欲しい場合は長方体を選ぶ、という戦略がチョイスできることが分かります。
サイコロのように確率分布が小さい場合は、分布を考えずとも経験で判断できると思います。しかし、膨大で複雑な確率パターンがある場合は、その確率分布を比較検討することで自分が望んだ結果を得やすくなるでしょう。
実際にサイコロを振ってデータを出して確かめたい時はこちらのサイトでダイスロールが可能です。ダイスロールはこちら。
<この記事のポイント>
・確率変数とは確率によって得られる値が格納されるもの
・確率分布とは確率変数のとる値と、その値をとる確率の全ての広がりのこと
・確率分布を知ることで「検定」や比較による選択が容易になる






Leave a Reply