ABテストの結果検証に必須！覚えておきたい「検定」のやり方

ウェブサイトを少しでもよくするため日々何かの改善をしていることでしょう。バナーを変えたり、デザインを変えたり、レイアウトを変えたり。例えばランディングページなどはこれまでちゃんと作り込んでいなかった場合、ちょっと作り込むだけで大きく結果が変わってきます。

では、ある程度作り込んでいるランディングページは大きく変わらないのでしょうか？それは違います。作り込んだランディングページも正しく効果を検証し、改善を積み上げていくことで大きく結果は変わります。いわゆるABテストをするわけですが、今回はABテストの結果を正しく検証するために「検定」についてご説明します。

検定とは

検定というと英検や簿記検定という方が一般には馴染みがあると思います。それとは別に統計の世界でも検定は存在します。統計で言うところの検定とは「統計的仮説検定」ともいい、確率を元に結論を導き出す手法です。ウェブでは細かい数値が得られるのでABテストとの相性が良く、データが得られやすいのでテスト結果の検証では必ず検定を用います。

ABテストなどの結果検証で検定が用いられるのには理由があります。検証にルールがあること、そして基準が明確になることにより、結果に主観による判断が入る余地がないことです。

ABテストがうまく機能しない理由に、正しく結果検証をしないことが挙げられます。それは検証に明確なルールがないためであり、数字の表面的な部分を見た発言権の大きい人の意見で収まってしまいがちです。つまり、一部の人間の主観で結果が決まってしまいます。これが経営者の主観であれば別に構わない、と思われるかもしれませんが、正しく検定を行うことでミスジャッジの回数を減らすこともできるのです。

検定の手順

検定の手順は以下の通りです。

１・仮説を立てる
２・判断基準を決める
３・確率を求める
４・基準を元に判断を下す

このようにまず最初に「仮説」を立てます。次にこの仮説が正しいと判断するための「基準」を決めます。そして実際に怒った事象の確率を検証し、この基準に照らし合わせて結論を導き出します。そしてこの結論を導き出すために「背理法」を使います。

「背理法」とは最初に立てた仮説が正しいことを前提としている検証し、その結果が仮説と矛盾することで前提が間違っているとする手法です。

１・仮説を立てる

まず仮説を立てるわけですが、「帰無仮説」と「対立仮説」の二つを立てる必要があります。

「帰無仮説」とは検定を行うために立てる仮説であり、「対立仮説」とは帰無仮説に対する仮説を表します。この仮説を立てる時は本来証明したい仮説を対立仮説にします。

例えば、広告のバナーでABテストを行うとした場合、本来証明したいことは「バナーAとバナーBのクリック率に違いがある」ことです。これが対立仮説となるため、帰無仮説では「バナーAとバナーBのクリック率に違いはない」ということになります。

どちらのバナーがよくクリックされるのだろうか？クリック率はいいのだろうか？

２・判断基準を決める

仮説が正しい、もしくは間違っているとする判断基準を先に決めます。結果が出た後に基準を決めてしまうと、そこに主観が入ってしまい客観的なジャッジができなくなります。

検定ではこの判断基準のことを有意水準と呼びます。これは「“滅多にない”と判断する確率の基準」であるため、求めた値がこの有意水準を超えると帰無仮説に誤りがある（棄却される）ことになります。一般的に有意水準は５％とされることが多いです。

３・確率を求める

仮説と基準が決まると、次は実際に仮説が正しいかを判断するための確率もしくは検定統計量（P値）を求めます。この検定統計量とはコインやサイコロなどのように確率が出るものではないもの（長さや重さなど）が検定対象である場合、その値を「検定するための値」に変換したものです。

この検定統計量は標準化したzや、少ないサンプルから求めるtなどがあり、検定統計量を求めることで対応する分布から確率を表すP値を導き出すことができます。

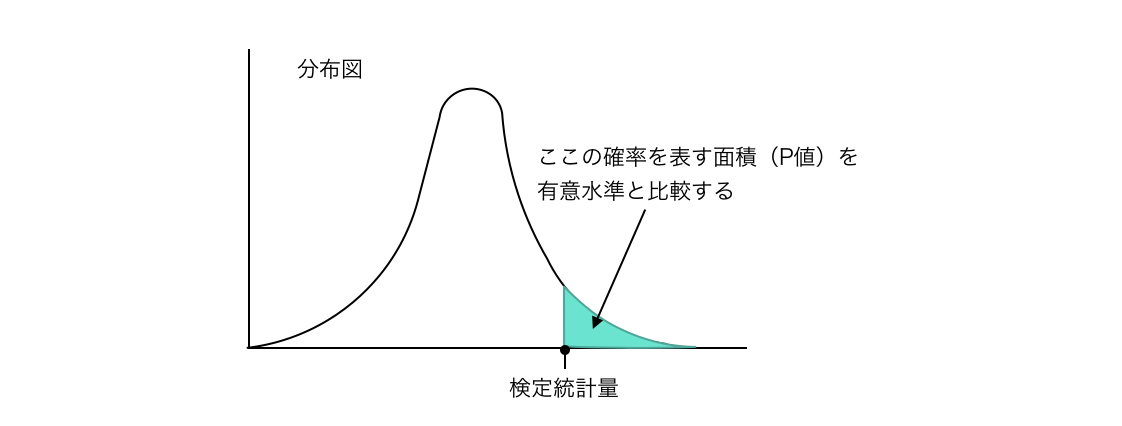
上図は横軸を統計量、縦軸を確率密度を表します。計算で求められた統計量以上の面積を求めることで確率を出すことができます。計算で求めるには積分をするのですが手間がかかるため、。標準正規分布表やt分布表といった対応する一覧表を使って確率を読み取ります。

４・基準を元に判断を下す

P値が算出されると、基準と照らし合わせます。P値が有意水準を下回っていれば帰無仮説が“滅多にない”であるということになります。このことから帰無仮説は棄却され対立仮説が採用されます。

注意すべきはP値が有意水準を下回らず帰無仮説が棄却されなかった場合です。これは帰無仮説が正しいことを証明しているのではなく、対立仮説が正しいとは言えないことを表します。このような結果の場合は新しい仮説を立てていく必要があります。

第１種の過誤と第２種の過誤

検定で得られる結果は絶対ではありません。検定を進める上で第１種の過誤と第２種の過誤という注意すべきポイントがあります。第１種の過誤とは本当は正しいのに誤って棄却してしまうことで、有意水準はこの第１種の過誤を犯す確率とも言えます。第２種の過誤とは対立仮説が正しい時に誤って帰無仮説を棄却しないことです。仮説の誤りを見つける検出力が低いことで、本当は誤っているのに間違った仮説を採用してしまうということです。

例えば裁判でいうのであれば、以下のようなものです。
・犯人が本当に犯行を自供しているが無罪と判決が出る（第１種の過誤）
・容疑者が本当は無罪なのに有罪判決が出る（第２種の過誤）

あくまでも例えですがこのような危険性も検定の時にはありえるということは理解しておく必要があります。

そしてこの二つはトレードオフの関係にあります。第１種の過誤を減らすべく有意水準を厳しいものにした場合、厳しくな多分だけ帰無仮説が棄却されにくくなります。逆に第２種の過誤を減らそうとする場合、有意水準が甘くしなくてはいけません。肝心なのはバランスをとるということになります。

まとめ

検定という言葉だけで聞くと何か複雑な手順が必要な感じもしますが、このように難しいことはありません。また統計検定量の算出はエクセルなど表計算ソフトでも簡単にできるので、検定を行わない手はありません。手順や仕組みを理解できれば間違うこともありません。

ABテストがうまくいかないと原因に、「テスト結果の検証をしない」ということが多くあります。結果検証をしないということはPDCAサイクルが回ることがなく、改善した気分になっているだけかもしれません。ウェブサイトを作り込めば作り込んでいくほど改善にはテストと検証が必要になってきます。効率的に改善ができるよう検定の仕方を理解しておきましょう。