
グーグルアナリティクスをはじめ、様々なデータを見る場合に比較を行うことが多々あります。戦略上のターゲットの分析での「この商品を5個購入した人は全体の何%なの?」といったことや、「平均購入金額が12,000円以上のユーザーの割合はどのくらい?」といった疑問を感じたことはないでしょうか。
自社の顧客を分析する上でも細かいセグメントは有効です。データの表面では見えないものを見えるようにして、正しいユーザーセグメントする上でも標準化を理解しておいた方が良いでしょう。
- 標準化とは
- 標準化を行う
- 標準化したデータの使い方
- まとめ
[目次]
標準化とは
データが複数ある場合、そこには平均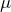 と分散
と分散 があります。平均はデータの合計をその個数で割った値であり、データ群の持つ一個の大きさをイメージで捉えるのに役に立ちます。分散はデータの散らばりを表し、データの大きさのばらつきを見ることができます。つまり分散が小さければデータ群はより集まっていることがわかります。
があります。平均はデータの合計をその個数で割った値であり、データ群の持つ一個の大きさをイメージで捉えるのに役に立ちます。分散はデータの散らばりを表し、データの大きさのばらつきを見ることができます。つまり分散が小さければデータ群はより集まっていることがわかります。
(関連記事:統計を活用してアクセス解析に挑む下準備として、分散と標準偏差を理解する)
このように平均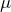 と分散
と分散 でデータのイメージを掴むことができるのですが、単位や平均値が異なる場合は単純に比較することはできません。
でデータのイメージを掴むことができるのですが、単位や平均値が異なる場合は単純に比較することはできません。
身近なものでわかりやすく言えば「国語」「数学」のテストの点数の比較があります。
Aさんが国語で75点、数学で76点であった場合どちらが順位が上と言えるでしょうか。教科が違うから単純に比較できないことがわかりますね。
この比較を単純に行うようにデータの変換を行うのが標準化なのです。
標準化を行う
それでは早速標準化を行ってみましょう。まず標準化を行うにはそれぞれの母集団(データ群)の平均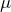 と標準偏差
と標準偏差 が必要です。(標準偏差
が必要です。(標準偏差 は√分散
は√分散 、つまり分散の平方根です。)
、つまり分散の平方根です。)
1・データの値から平均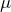 を引く。
を引く。
2・1を標準偏差 で割る。
で割る。
これは値と平均の差分を求め、それをデータのばらつき度合いで割ったもので、この値をZ値(基準値や標準化得点)と言います。
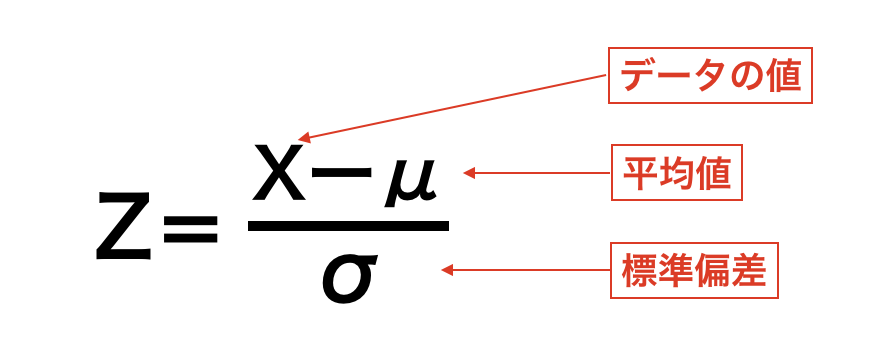
また、
Zは平均0、分散1の標準正規分布に従う
と言うことから、標準化されたデータは標準正規分布と同じ確率分布になるため比較が容易になることもイメージがつくでしょう。
ちなみに前述の「国語」「数学」に平均と分散がわかっているとし、それぞれのテストは独立している(互いに影響がない状態)ものとして
| 国語 | 数学 | スペイン語 | |
| 得点 | 75 | 76 | 50 |
| 平均 | 50 | 70 | 72 |
| 標準偏差 | 15 | 10 | 8 |
国語のZ値は、 Z = (75-50) / 15 = 1.66
また数学のZ値は、 Z = (76-70) / 10 = 0.6
スペイン語のZ値は、 Z = (50-72) / 8 = -2.75
このようにZ値を持って比較すると国語の得点がより良い得点であることがわかる。ちなみに、このZ値を10倍にして50を加算したものが偏差値となる。
この例で言えば、国語の偏差値は66、数学は56、スペイン語は23であることがわかる。
標準化したデータの使い方
あるデータが正規分布に従うと仮定できる場合、このデータを標準化することで「標準正規分布表」を用いて確率を求めることができます。この確率は「標準正規分布に従うZがとる値がz以上となる確率P(Z≧z)」を表します。
例えば複数個まとめ買いができる商品Aがあるとします。この商品は一人あたり平均3.6個の購入があり、標準偏差は3の正規分布に従います。この時商品Aを5個以上購入している人は何%いるでしょうか。
1・まず、5個購入を標準化します。すると、Z = (5 – 3.6) / 3 = 0.46
2・次にZが0.46をとる確率を標準確率分布表を使って算出します。
見方はZの少数点第一位までの値を一番左で探します。そしてその行と、小数点第二位の示す列の交差する値がZから求める確率となります。先ほどのZ値は0.46でしたので0.4の行と.06の列の交わる部分の0.323、つまり32.3%が5個以上購入している人の割合となります。
| z | .00 | .01 | .02 | .03 | .04 | .05 | .06 | .07 | .08 | .09 |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0.500 | 0.496 | 0.492 | 0.488 | 0.484 | 0.480 | 0.476 | 0.472 | 0.468 | 0.464 |
| .1 | 0.460 | 0.456 | 0.452 | 0.448 | 0.444 | 0.440 | 0.436 | 0.433 | 0.429 | 0.425 |
| .2 | 0.421 | 0.417 | 0.413 | 0.409 | 0.405 | 0.401 | 0.397 | 0.394 | 0.390 | 0.386 |
| .3 | 0.382 | 0.378 | 0.374 | 0.371 | 0.367 | 0.363 | 0.359 | 0.356 | 0.352 | 0.348 |
| .4 | 0.345 | 0.341 | 0.337 | 0.334 | 0.330 | 0.326 | 0.323 | 0.319 | 0.316 | 0.312 |
| .5 | 0.309 | 0.305 | 0.302 | 0.298 | 0.295 | 0.291 | 0.288 | 0.284 | 0.281 | 0.278 |
| .6 | 0.274 | 0.271 | 0.268 | 0.264 | 0.261 | 0.258 | 0.255 | 0.251 | 0.248 | 0.245 |
| .7 | 0.242 | 0.239 | 0.236 | 0.233 | 0.230 | 0.227 | 0.224 | 0.221 | 0.218 | 0.215 |
| .8 | 0.212 | 0.209 | 0.206 | 0.203 | 0.200 | 0.198 | 0.195 | 0.192 | 0.189 | 0.187 |
| .9 | 0.184 | 0.181 | 0.179 | 0.176 | 0.174 | 0.171 | 0.169 | 0.166 | 0.164 | 0.161 |
| 1.0 | 0.159 | 0.156 | 0.154 | 0.152 | 0.149 | 0.147 | 0.145 | 0.142 | 0.140 | 0.138 |
| 1.1 | 0.136 | 0.133 | 0.131 | 0.129 | 0.127 | 0.125 | 0.123 | 0.121 | 0.119 | 0.117 |
| 1.2 | 0.115 | 0.113 | 0.111 | 0.109 | 0.107 | 0.106 | 0.104 | 0.102 | 0.100 | 0.099 |
| 1.3 | 0.097 | 0.095 | 0.093 | 0.092 | 0.090 | 0.089 | 0.087 | 0.085 | 0.084 | 0.082 |
| 1.4 | 0.081 | 0.079 | 0.078 | 0.076 | 0.075 | 0.074 | 0.072 | 0.071 | 0.069 | 0.068 |
| 1.5 | 0.067 | 0.066 | 0.064 | 0.063 | 0.062 | 0.061 | 0.059 | 0.058 | 0.057 | 0.056 |
まとめ
標準化することでデータの比較が容易になるだけでなく、特定の条件化でのその割合を算出することもできることがお分かりいただけたと思います。表面では見えないデータの本質を理解する上でもこのようなデータの変換ができることは大変重要でしょう。
標準化したデータは全体を表すものではなく、全体の中でのデータのポジションを見るようなものです。購入数や購入金額といったユーザーの条件を元に調べ、ユーザー分析を行うなど標準化の活用方法は色々あります。
実は標準化しなくても表計算ソフトをサクッと使えるのであれば、データベースからソートや抽出を使えば標準化せずに割合を調べることは可能です。ただ知りたいユーザー条件が変わればその都度表計算ソフトを動かす必要があります。標準化は平均値や標準偏差がわかっていれば表を見るだけですぐに確率が理解できるので、効率的なマーケティングにも有効な手立てと言えるでしょう。
<この記事のポイント>
・異なるデータを比較する際は標準化を行い、標準正規分布に従わせる。
・標準正規分布表を活用することで、特定の値での割合を導き出すことができる。
・データの本質を見抜く上でも標準化は有効。






Leave a Reply